您现在的位置是：首页 > IT基础架构 > 软件与服务 >
二级供应链系统库存策略的系统动力学研究
摘要以系统动力学模型为框架，提出了以预测平均值和预测误差标准差为基础确定订货量的库存控制策略，并以库存服务水平和库存成本为目标，对所提出的库存策略中的政策性参数进行了组合优化。...
供应链中的一个焦点问题就是牛鞭效应。20世纪60年代初，Forrest采用系统动力学原理，首先分析了消费需求波动沿供应链向上游企业逐级放大的系统特性。1984年，美国麻省理工学院的Sterman教授设计了啤酒游戏，证实了牛鞭效应的存在，并认为该效应是供应链成员系统性、非理性行为和对反馈信息的错误理解造成的。20世纪90年代初，宝洁、通用、福特、克莱斯勒、惠普、康柏等公司在研究其产品的市场销售量和分销商订货量时也发现了牛鞭效应。
对供应链牛鞭效应现象做出较为系统全面分析的是H．L．Lee。他建立了供应链牛鞭效应的量化模型，研究结果认为牛鞭效应是供应链成员战略性行为相互影响的产物，是对各自局部利益的最优化决策的博弈结果。H．L．Lee同时指出，供应链成员对需求信息的处理技术、批量订贷方式、价格波动、预计供应量不足导致的零售商之间的短缺博弈是导致供应链牛鞭效应的四个主要因素。我国学者认为这四项因素对牛鞭效应的影响程度在不同的场合有效性不一，信息共享也不总是有效。因此对供应链库存的影响还有更深层次的因素。本文认为结构决定行为，产生牛鞭效应的主要原因在于供应链系统的组织和运作模式，因此论文从整体协调的角度探讨二级供应链的库存策略及其优化问题。
传统的库存控制是通过存储论模型来解决的，这种方法有其自身的优点，但也有缺点。其主要不足是假设需求服从某种分布，计算复杂、不能直观地反映两级库存之间的相互影响。实际中，需求不一定服从某种分布，可能是一系列不规则数据，也可能呈现某种趋势且同时伴有随机性，这样传统的库存控制策略较难直接发挥作用。系统动力学模型可以有效地解决供应链库存策略制定问题，并且分析过程比较直观和易于理解。
本文以超市配送中心系统为背景，建立二级供应链库存的系统动力学模型，从系统运行机理出发，研究不同类型的市场需求的情况下。预测技术和信息共享等对供应链牛鞭效应的影响，并利用遗传算法对供应链库存策略进行优化。
2 超市配送中心系统运作模式和控制目标
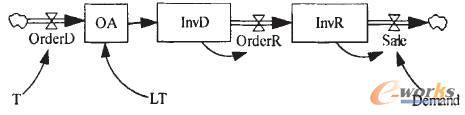
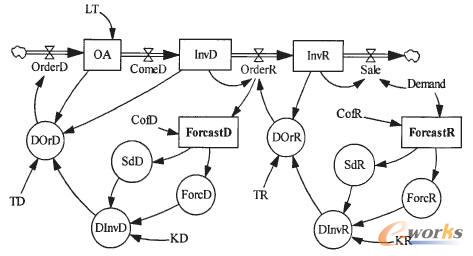
配送中心的建立是物流运作技术发展的结果，零售商向配送中心订货可以认为是立即补货(即每天晚上订货第二天早上到货)，配送中心以一定的周期(T)向其供应商订货，提前期为LT，并且订货总能够被满足。于是可以得到超市配送中心库存系统的基本系统动力学模型如图1所示。
图1 配送中心系统的基本系统动力学模型
图中，InvD为配送中心的库存，InvR为零售商的库存(即货架上商品的存量)，Demand为市场需求，LT为配送中心订货的提前期，T为配送中心的订货周期。OA为在途货物，即描述了订货的物质延迟。Sale为每天的销售量，应尽量使其等于需求量Demand，否则就发生缺货现象。
这种情况下，如果处理不当会产生“牛鞭”效应，并且会伴随着大量的缺货。为了克服这种现象，并从长期上保证整个供应链系统的效益最佳，确定零售商和配送中心的库存控制策略OrderD和OrderR非常重要。这里采用库存控制的基本目标，即缺货量最小和库存相关成本最低。由于零售商每天订货，配送中心以固定周期T订货，因此在考察区间一定的情况下，订购费用都是相同的，所以只考虑库存维持费用。
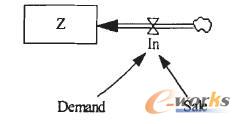
缺货量最小可用缺货数量来表示：
描述这项指标的系统动力学协流结钩如下：
图2 缺货最小的协流结构
上述协流结构的系统动力学方程如下：
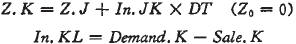
库存维持费用可用配送中心的库存维持费用和零售商的库存维持费用加权之和来描述：
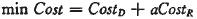
其中，a为权重系数。
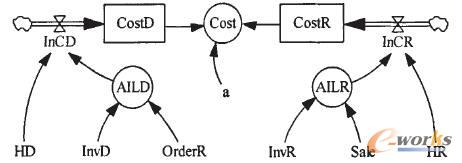
描述这项指标的系统动力学协流结构如下。
图3 库存维持费用最小的协流结构
图中，HD为配送中心单位产品单位时间的库存维持费用(元／件／天)，HR为零售商单位产品单位时间的库存维持费用(元／件／天)。AILD和AILR分别为配送中心和零售商的平均库存。
这个协流结构的系统动力学方程如下：
3 超市配送中心系统的库存控制策略分析
通过上述分析可知，这个系统涉及两个库存控制策略，一是零售商向配送中心的订货策略OrderR，另一个是配送中心向供应商的订货策略OrderD。现对其分析如下：
(1)零售商的订货策略OrderR
零售商组织订货的依据是什么呢？很显然，一是根据需求情况，二是目前货架上还有多少商品，即OrderD＝f(InvR，Demand)。目前的存货量InvR可以通过观察或库存记录获得，需求量可以通过预测获得。为了应付不确定性还要考虑必要的安全库存。于是可得下一时刻库存水平的目标值(DInvR)：
DInvR＝Forcast＋SaftyStock＝ForcR＋KR×SdR
其中，ForcR为预测值，SdR为预测误差的标准差，KR为安全系数。
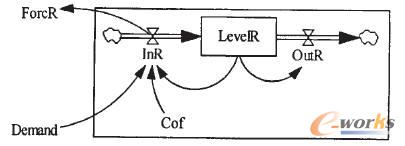
理论上可以采用任何预测方法对未来的需求量进行预测。在此，采用指数平滑法预测，其系统动力学模型如图4所示。
图4 指数平滑预测的系统动力学模
相应的系统动力学方程如下：
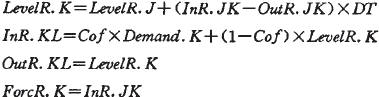
Col为平滑系数。如果对InR再进行一次平滑，并按二次指数平滑的规则获得预测方程：ForcR＝a＋bt，即为二次指数平滑预测。本文采用二次指数平滑法对未来的市场需求进行预测。
预测误差的标准差可用下式计算：
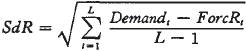
其中，L为仿真区间长度。
有了下一时刻库存水平的目标值(DinvR)，就可以按照常规的库存策略进行补货：
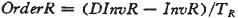
即在给定的库存调节时间TR内，将库存补充至目标水平DInvR。在此采取立即补货方式，取TR＝1，即每次订货都将库存补充到期望水平。
(2)配送中心的订货策略OrderD
分两种情况讨论配送中心的订货策略。首先，信息没有共享，配送中心根据零售商的订货量(OrderR)和其自身的库存水平进行订货；其次，信息共享，配送中心根据最终需求(Demand)和其自身的库存水平组织订货。
同样，采用二次指数平滑法对零售商的订货量(OrderR)或最终需求(Demand)做出预测，得到下一个订货周期内的库存目标DInvD。
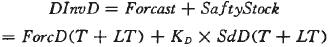
其中，ForcD(T＋LT)和SdD(T＋LT)分别为配送中心在(T＋LT)区间内需求的预测值和预测误差的标准差。由于零售商是每天订货，所以采用对每天的需求预测然后累加的办法获得。如果对每天需求采用二次指数平滑的预测方程为：F＝a＋bt，预测误差的标准差为跗D。则ForcD(T＋LT)和SdD(T＋LT)可以计算如下：
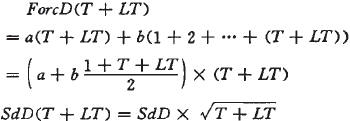
有了下一时刻库存水平的目标值(DInvD)，就可以按照常规的库存策略进行补货：
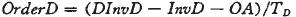
即在给定的库存调节时间n内，将库存补充至目标水平DInvD。这里采取立即补货方式，取TD＝1，即每次订货都将库存补充到期望水平。另外，考虑到在订货提前期大于订货周期的情况下，在订货决策时还有即将到货在途货物，所以OA也出现在表达式中。
4 超市配送中心系统的库存控制策略优化研究
综合上述过程，可得到如下系统仿真模型。
图5 二级供应链库存系统模型
图中，DInvD和DInvR是配送中心和零售商的目标库存，DOrD和DOrR是配送中心和零售商的期望定货量。计算方程如下：
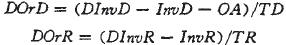
OrderD和OrderR是配送中心和零售商实际拿到的货物量。计算方程如下：
即假设配送中心总是可以足额拿到所定的货物。而零售商能拿到的货物要受配送中心仓库中是否有货的限制。
另外，需要指出的是，Sale和OrderR是需求被满足的量，而Demand和DOrR才是需求量。所以，在信息非共享情况零售商和配送中心预损l的依据分别是Demand和DOrR，而在信息共享情况零售商和配送中心预测的依据都是Demand。
综上所述，可以得到超市配送中心系统的4个控制参数：同库存服务水平相关的安全系数KR和KD。同预测过程相关的指数平滑系数CofR和CofD。通过合理匹配这4个参数，来权衡用缺货表示的库存服务水平和库存维持成本。
另外，考虑供应链上下游之间需要协调，如果其成员频繁调节各项控制参数会给上下游带来损失。所以在政策方案设计时，除了政策参数的自由组合外，还考虑通过预测理论确定指数平滑系数CofR和CofD，而只将安全系数KR和KD作为政策参数进行优化。
不同的需求特性要有不同的政策参数来匹配，所以本文考虑三种需求特性。一是没有趋势性的随机波动，二是明显的趋势性变化，三是较长周期性交化。三种情况具体描述如下：
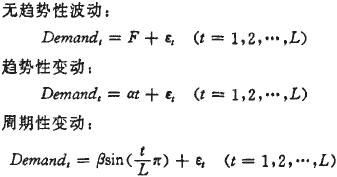
其中，α、β、F为常数，εt为噪声函数，L为仿真区问长度。这里，α＝0.8，β＝10，F＝10。ε设定为均值μ＝10、方差σ＝3的正态分布函数。
为了便于分析问题，取配送中心的订货提前期LT＝3天，订货周期T＝5天。配送中心的库存维持费用HD＝0.02元／件／天，零售商库存维持费用HR＝0.05元／件／天。系缔的初始状态设为配送中心库存为20件，零售商库存为120件，没有在途货物。取仿真区间长度L＝365天。差分步长DT＝1天。对于以上三种需求特性，在信息共享和非共享两种协调机制下进行控制参数的组合优化研究。
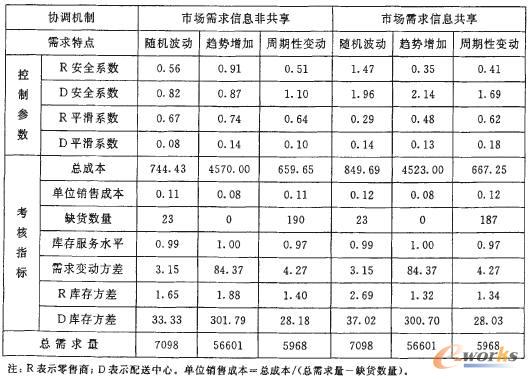
政策优化采用遗传算法和人工试凑法相结合的方式寻求满意解。系统的仿真结果如表1所示。
表1 四参数组合优化结果
通过控制参数的组合可以达成满意的库存维持成本和库存服务水平。从参数优化的过程来看，能够达成相当水平的库存维持成本和库存服务水平的参数组合有多种，换言之，目标函数对有些参数的变化不是很敏感，说明在图5所示的供应链组织模式和基于预测的订货策略下，供应链系统是稳定的。从总体上看，指数平滑预测可以较好地适用趋势性和长周期特点的需求情况；信息共享可以在一定程度上降低成本和削弱牛鞭效应，对库存服务水平影响不大。
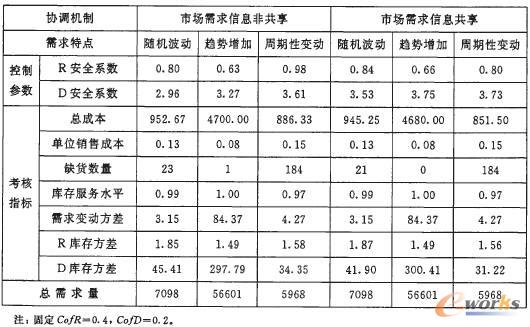
如果考虑供应链的协调。变化的参数不宜过多，参数的变化也不宜过于频繁。所以。上下游应通过协商固定一些参数。我们考虑双方可以通过预测理论和需求数据的变化特征，确定指数平滑系数CofR和CofD，将二者作为非政策参数，对KR和KD进行组合优化。这里，取CofR＝0.4．CofD＝0.2。计算结果如下表所示。
表2 二参数组合优化结果
可见，固定平滑系数对成本和缺货的影响不是很大，尤其是在趋势增加的需求特点情况下的影响更小。
为了进一步考察研究结果的适用性，本文还分析了考虑博弈行为条件下，优化结果的实施问题。仿真结果表明，优化结果不仅使得供应链整体效益增加，还可以同时降低上下游的成本和缺货。说明优化结果对供应链上下游都有益，有利于在实际管理中实施。如果只对单方有益就需要制定相应的协调机制来权衡上下游的利益，进而达到实际实施的效果。
5 结论与展望
本文以系统动力学的原理和方法为工具，对于二级供应链分散库存模式和定期订货系统，提出了利用指数平滑预测法对需求进行预测，以预测平均值和预测误差标准差为基础确定订货量的库存控制策略，并以库存服务水平和库存成本为目标，对所提出的库存策略中的政策性参数进行了组合优化。研究结果表明，无论需求的特征如何，对于二级供应链分散库存模式和定期订货系统，指数平滑预测法以及本文所提出的基于指数平滑预测法的库存控制策略都具有较好的适用性，并可以通过政策性参数的合理组合达到满意的绩效目标。
供应链库存控制是一项复杂的系统性工作，涉及组织模式、控制策略和政策性参数等三个层面的问题，本文是从实际应用和可操作性的角度研究给定组织模式下的库存策略问题，虽然得出的结论是基于对具体个案的仿真分析，但是由于所建立的系统动力学模型具有一般性的特点，仿真过程中又对个案中给定的特征参数进行了大量的灵敏度测试，所以本文得出的结论对于给定模式的供应链库存系统具有一般性的指导和借鉴意义。另外，由于本文所建立的模型和仿真过程都具有较好的可理解性和较好的可操作性，所以容易被实际管理所采用。
(本文不涉密)
责任编辑：
特别推荐
 |
站点信息
- 运营主体：中国信息化周报
- 商务合作：赵瑞华 010-88559646
- 微信公众号：扫描二维码，关注我们
