闭环供应链中逆向物流供应商选择模型研究

    随着环境的日益恶化和政府强制法律的相继出台，传统供应链中的核心企业越来越多地关注产品的回收和再利用，开始主动承担自身的环境责任，出现了原材料、在制品和产成品从消费地向生产地的大规模流动，所谓的逆向供应链也应运而生。传统供应链与逆向供应链的有机结合形成了闭环供应链，逆向物流作为闭环供应链的一个重要回路正日益引起各方关注。从提升核心能力的角度出发，实现逆向物流业务外包从而更专注于自身的核心领域，已成为闭环供应链中核心企业的现实选择。目前关于逆向物流供应商选择的研究还非常贫乏，而选择模型在整合供应商优选过程中又处于核心地位。

1 已有研究成果述评

    关于供应商选择模型的研究，国外比较有代表性的相关文献主要包括:Yahya & Kingsman(1999)运用层次分析法，试图得到供应商评价准则及其相应权重；Manoj Kumar(2004)利用模糊优化理论对供应商进行选择，从三个方面建立约束:最小净成本、最大满意度、最小延迟时间；Zeger(2002)对供应商选择模型进行了总结分析，主要包括:基于活动的成本分析法(Activity Based Costing)、线性加权法(Linear Weighting)、数学规划法(Mathematical Programming)及统计方法(Statistical)；Joe Zhu(2004)利用买卖双方二阶段博弈模型，对DEA模型进行了简化，建立了一个效率区间，对供应商进行选择。国内对相关领域的研究始于上世纪90年代末，借鉴国外的理论成果并于中国实际相结合，供应商选择模型主要包括模糊层次分析法、数据包络分析法、作业成本法、欧式范数及神经网络法(王家顺，2001；段永瑞，2004；王刊良，2001；王瑛，2002；仲维清，2003)。

    单一的供应商选择模型各有弊端，针对单一供应商选择模型的缺陷，近年来国内学者也进行了一些集成多种方法的综合研究(常丹，2004；王旭坪，2004；杨玉中，2006；史学峰，2006)，由于方法本身的合理性需要进一步的理论证明和实践检验，导致了这些集成模型在逆向物流供应商选择过程中的应用相当贫乏。总体而言，选择模型需要和选择标准相匹配，沿着综合多种方法集成研究的思路，本文经过理论推导采用基于DEA数据处理的AHP模型(DEA-AHP)对逆向物流供应商进行选择，为使选择模型的研究推进一步，论文结合实际算例对DEA-AHP护模型的选择结果进行了统计检验，直观分析了新选择模型的优点，界定了选择模型的适用范围。

2 闭环供应链中逆向物流供应商选择模型设计思路

    闭环供应链中核心企业与逆向物流供应商合作不仅强调对废弃物的回收利用，更强调通过资源缩减、翻新、改制和再生循环等方式，实现节约资源、保护环境和增强竞争力等目标。已有的研究表明，长期的战略性合作需要以效率为基础的持续发展能力的保证。而数据包络分析(DEA)依据“生产前沿面”来比较各决策单元之间的相对效率，能够遴选出具有很好发展潜力的合作伙伴。但由于DEA有效决策单元对应的指标数据是相应多目标规划问题的Perato有效解，当评价指标较多时，常常会出现多个决策单元相对效率值为1的情况，这种情况随着投入产出指标的增加变的越来越明显，这在一定程度上限制了排序方法区分决策单元的能力。

    另外，层次分析法(AHP)作为系统工程中将非定量事件作定量分析的一种简便而有效的模型，它具有能将决策者对复杂系统的决策思维过程实行数量化，且具备所需定量数据较少，易于计算，可解决多目标、多层次、多准则的决策问题等优点，但由于AHP主观性太强的缺陷，也限制了其应用范围。

    数据包络分析法和层次分析法两种模型本身是有内在联系的，同时又有各自的优点：DEA可以为生产企业选出具有持续发展潜力的逆向物流供应商，体现效率评价的优点。AHP可以在DEA选择的基础上，对选择结果进行进一步优化。由于单一选择模型的局限性，沿着综合多种方法集成研究的思路，本文经过数学推导和统计检验，提出基于DEA数据处理的AHP模型(DEA-AHP)对逆向物流供应商进行选择，既增加了AHP判断矩阵的客观性，又提高了DEA对有效单元的区分精度。

3 基于DEA 数据处理的AHP选择模型(DEA-AHP)的理论推导

    假设共有n个备选供应商，每个供应商有二个投入和s个输出，其中Xij表示第i个供应商的第j个投入，Yij表示第j个供应商的第r个产出，应用C2R模型对第j个供应商(1≤j≤n) 进行DEA效率评价，经过使用Charnes Cooper变换，可以化为一个等价的线性规划模型：

    

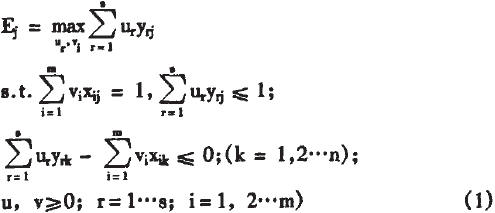
    定义：若线性规划模型(1)的最优解u*和v*满足Ej＝1，那么供应商j是有效的。

    从所用供应商中任选两个作为研究对象，分别用A和B来表示，单独对这两个供应商使用DEA模型，由式(1)可得：供应商A的相对效率定义为EAA，其中：

    

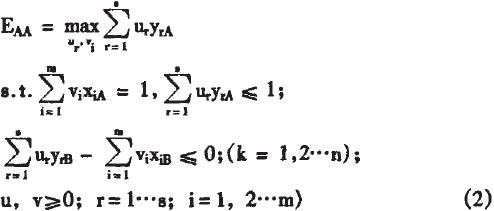
    从模型中可以解出一对和ur，vi以及一个正的松弛变量，如果决策单元A是有效率的，那么公式(2)的松弛变量SA＝0，同时SB≥0；否则，SB＝0，SA≥0，其他变量为0。

    因此，如果存在任意一对投入和产出(i，r)约满足Yra/Xia≥Yra/Xib，那么EAA＝1，否则，EAA＝Max(i，r)，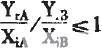
    同理，可求出供应商B的相对效率为：EBA＝，在计算供应商B的相对效率过程中，引入非阿基米德无穷小量ε，使判断松驰变量的工作大大简化。

    

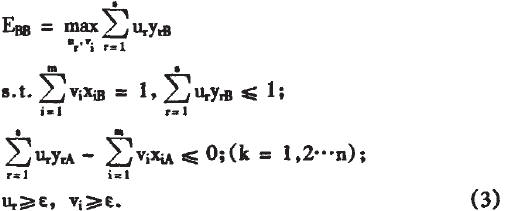
    由于只存在两个供应商A和B，显然EAA＝EAB，EBB＝EBA，A和B两个供应商之间的相对效率比值为EAA/EBB。

   基于以上推导，可以得出层次分析法的判断矩阵的输入值，即为任意两个供应商相对效率的比值：ajk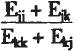＝，同时，ajj＝1。

    因此，层次分析法的判断矩阵对角线上的数值均为1，ajk的值决定着供应商j和供应商k的相对效率，如果ajk＜1，那么供应商j就是相对无效率的，同理可得：

    

    那么，akj/1ajk，层次分析法的判断矩阵就可表示为：

    

    对上阶段所得到的判断矩阵A，计算最大的特征值、和特征向量ω(Aω＝λω)，即为供应商相应的排序向量，第j个供应商的特征向量就可以作为衡量其相对重要性的权重。因此，最大特征向量所对应的供应商是效率排序的最优解。

    单纯的DEA模型运算结果会产生出多个具有效率的决策单元，这种现象随着投入、产出数量的增加而更加明显，这必然影响投入产出多目标优化过程中的帕累托最优解，本文提供的DEA-AHP选择模型有效的解决了这一问题，通过判断矩阵得出的特征向量的大小，可以清楚的为各决策单元排序。DEA-AHP与DEA的结合应用，可以有效地提高传统DEA模型的区分精度，达到供应商选择结果的优化。

3 基于DEA 数据处理的AHP选择模型(DEA-AHP)的理论推导

    假设共有n个备选供应商，每个供应商有二个投入和s个输出，其中Xij表示第i个供应商的第j个投入，Yij表示第j个供应商的第r个产出，应用C2R模型对第j个供应商(1≤j≤n) 进行DEA效率评价，经过使用Charnes Cooper变换，可以化为一个等价的线性规划模型：

    

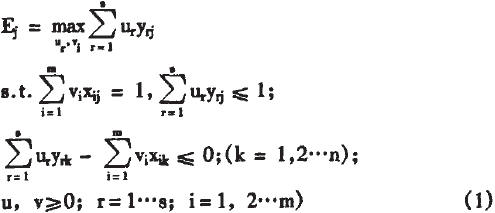
    定义：若线性规划模型(1)的最优解u*和v*满足Ej＝1，那么供应商j是有效的。

    从所用供应商中任选两个作为研究对象，分别用A和B来表示，单独对这两个供应商使用DEA模型，由式(1)可得：供应商A的相对效率定义为EAA，其中：

    

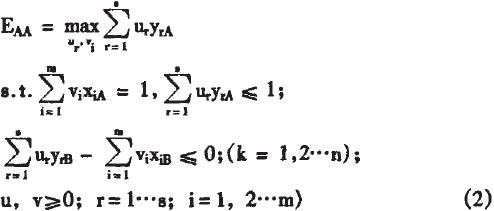
    从模型中可以解出一对和ur，vi以及一个正的松弛变量，如果决策单元A是有效率的，那么公式(2)的松弛变量SA＝0，同时SB≥0；否则，SB＝0，SA≥0，其他变量为0。

    因此，如果存在任意一对投入和产出(i，r)约满足Yra/Xia≥Yra/Xib，那么EAA＝1，否则，EAA＝Max(i，r)，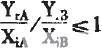
    同理，可求出供应商B的相对效率为：EBA＝，在计算供应商B的相对效率过程中，引入非阿基米德无穷小量ε，使判断松驰变量的工作大大简化。

    

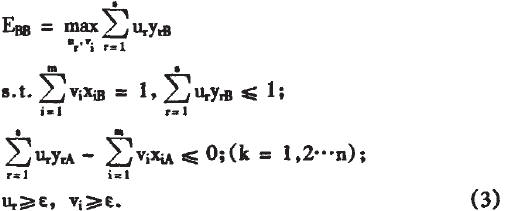
    由于只存在两个供应商A和B，显然EAA＝EAB，EBB＝EBA，A和B两个供应商之间的相对效率比值为EAA/EBB。

   基于以上推导，可以得出层次分析法的判断矩阵的输入值，即为任意两个供应商相对效率的比值：ajk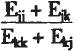＝，同时，ajj＝1。

    因此，层次分析法的判断矩阵对角线上的数值均为1，ajk的值决定着供应商j和供应商k的相对效率，如果ajk＜1，那么供应商j就是相对无效率的，同理可得：

    

    那么，akj/1ajk，层次分析法的判断矩阵就可表示为：

    

    对上阶段所得到的判断矩阵A，计算最大的特征值、和特征向量ω(Aω＝λω)，即为供应商相应的排序向量，第j个供应商的特征向量就可以作为衡量其相对重要性的权重。因此，最大特征向量所对应的供应商是效率排序的最优解。

    单纯的DEA模型运算结果会产生出多个具有效率的决策单元，这种现象随着投入、产出数量的增加而更加明显，这必然影响投入产出多目标优化过程中的帕累托最优解，本文提供的DEA-AHP选择模型有效的解决了这一问题，通过判断矩阵得出的特征向量的大小，可以清楚的为各决策单元排序。DEA-AHP与DEA的结合应用，可以有效地提高传统DEA模型的区分精度，达到供应商选择结果的优化。

转载：感谢您对网站平台的认可，以及对我们原创作品以及文章的青睐，非常欢迎各位朋友分享到个人站长或者朋友圈，但转载请说明文章出处。