基于数据挖掘的启发式抽样方法研究

　　引 言

　　数据挖掘技术(data mining)的产生和发展不是为了替代传统的统计分析技术，相反它为统计学的延伸和扩展提供了广阔的舞台。在数据挖掘的数据预处理过程中，大规模数据集是数据挖掘高效实现的障碍。宽表数据往往是几十万，上百万级记录的，要对所有数据进行训练，时间上很难满足要求了。抽样技术作为一项基本统计技术应用在数据挖掘中。

　　抽样(Sample)是从大量的数据中抽取与探索问题有关的数据子集，这个样本应该包含足够的信息，又易于处理。在目前海量的数据中，数据分布参差不齐。传统的抽样方法传统的抽样方法抽样单一，存在许多缺点，其中最大的不足就是抽样误差比较大，抽取到的样本数据存在不确定性，很难真实准确的反应原始数据的情况。

　　本文通过对传统的抽样方法进行研究，提出一种基于数据挖掘的启发式抽样方法。结合数据挖掘，挖掘数据的重要程度，并赋予权值，结合权值计算方法，对分层抽样方法进行改进，将权值计算融入分层抽样中的比例分配之中。按照计算的权值大小，进行比例分配，从而取得相对比较精确的样本数据。

　　1 常用抽样方法介绍

　　对数据进行抽样很有必要，不同的数据抽样方法对训练结果模型的精度有很大影响。可以考虑用一些数据浏览工具，统计工具对数据分布做一定的探索，在对数据做充分的了解后，再考虑采用合适的数据抽样方法，抽取样本数据进行建模实验。目前几种常用的抽样方法：

　　简单随机抽样(simple mndom sampling)，系统抽样(systematic sampling)，整群抽样(cluster sampling)，分层抽样(stratified sampling)。

　　2 分层抽样核心思想

　　分层次随机化抽样方法仍占主流地位，一直被视为标准的估计方法。其研究的核心仍然是在已有域中样本的条件下，如何更有“效率”的增加样本单元，以满足估计精度的要求。当前的主要方法有层层抽样法，ABC法，样本追加法和广义回归估计法。

　　2.1 分层抽样(类型抽样)

　　先将总体中的所有单位按照某种特征或标志划分成若干类型或层次，然后再在各个类型或层次中采用简单随机抽样或系用抽样的办法抽取一个子样本，最后，将这些子样本合起来构成总体的样本。

　　2.2 两种方法

　　分层抽样是把异质性较强的总体分成一个个同质性较强的子总体，再抽取不同的子总体中的样本分别代表该子总体，所有的样本进而代表总体。

　　(1)先以分层变量将总体划分为若干层，再按照各层在总体中的比例从各层中抽取。

　　(2)先以分层变量将总体划分为若干层，再将各层中的元素按分层的顺序整齐排列，最后用系统抽样的方法抽取样本。

　　2.3 分层标准

　　(1)以调查所要分析和研究的主要变量或相关的变量作为分层的标准。

　　(2)以保证各层内部同质性强、各层之间异质性强、突出总体内在结构的变量作为分层变量。

　　(3)以那些有明显分层区分的变量作为分层变量。

　　2.4 分层的比例问题

　　(1)按比例分层抽样：根据各种类型或层次中的单位数目占总体单位数目的比重来抽取子样本的方法。

　　(2)不按比例分层抽样：有的层次在总体中的比重太小，其样本量就会非常少，此时采用该方法，主要是便于对不同层次的子总体进行专门研究或进行相互比较。如果要用样本资料推断总体时，则需要先对各层的数据资料进行加权处理，调整样本中各层的比例，使数据恢复到总体中各层实际的比例结构。

　　3 数据挖掘中的赋予权值的方法

　　数据挖掘则侧重于对事务中蕴涵的未知规律进行发现。通过数据挖掘，对数据进行分析，发觉数据的重要程度，并根据数据的重要程度，采取合适的权值计算方法，将权值赋予数据。特征越重要，所赋予的权值越大，而不太重要的特征赋予较小的权值。有时，这些权值根据特征的相对重要性的领域知识确定。

　　4 基于数据挖掘的启发式抽样方法

　　传统的抽样方法采取单一的抽样方法，存在许多缺点，其中最大的不足就是抽样误差比较大。抽取得到的样本很难真实准确的反应原始数据的情况，因为在抽样研究中只取总体的一部分作为研究对象，所以样本的选取事关重要。在这里我们对传统的分层抽样方法进行改进，提出一种新的抽样方法，采取基于数据挖掘的启发式抽样方法。

　　简单的按各级次级总体占总体的单位数目来确定抽取数目的比重来抽取样本，具有不确定定性。不同的次级总体中的样本在总体中的重要程度不同，为了能够使抽取的样本精确的反映总体的特征，我们应当通过数据挖掘先确定次级总体的重要程度，再根据重要程度的差别，将不同的次级总体赋予一定的权值，根据权值计算应当抽取的数据比例。其核心思想为：

　　(1)采用分层抽样(stratified sampling)，先将总体的单位按某种特征分为若干次级总体(层)。分层可以提高总体指标估计值的精确度，它可以将一个内部变异很大的总体分成一些内部变异较小的层(次总体)。每一层内个体变异越小越好，层内变异则越大越好。

　　(2)采用数据挖掘技术，对分得的次级总体的数据进行分析。分析各个不同的次级总体的重要程度，采取赋予权值的算法，按照重要程度将次总体加权。

　　(3)按照所加权的比例，计算出应从次级总体中抽取的样本比例数目。

　　(4)按照比例抽取能够精确的反映总体的特征的样本进行下一步的研究。

　　5 信息损失与样本容量的确定

　　5.1 抽样与信息损失

　　一旦选定抽样技术，就需要选择样本容量。较大的样本容量增大了样本具有代表性的概率，但也抵消了抽样的带来的许多好处。反过来，使用较小容量的样本，可能丢失模式，或检测到错误的模式。图1a显示包含8000个二维点的数据集，而图1b和图1c显示从该数据集抽取的容量分别为2000和500的样本。该数据集的大部分结构都出现在2000个点的样本中，但是许多结构在500个点的样本中丢失。

　　图1 抽样丢失结构的例子

　　5.2 确定适当的样本容量

　　为了解释大致确定合适的样本容量需要系统的方法，考虑下面的任务：给定—个数据集，它包含少量容量相等的组。从每组至少找出一个代表点。假定每个组内的对象高度相似，但是不同组中的对象不太相似。还假定组的个数相对较小(例如，10个组)。2a显示了一个理想簇(组)的集合，这些点可能从中抽取。

　　使用抽样可以有效地解决该问题。一种方法是取数据点的一个小样本，逐对计算点之间的相似性，然后形成高度相似的点组。从这些组每组取一个点，则可以得到具有代表性的点的集合。然而，按照该方法，我们需要确定样本的容量，它以很高的概率确保得到期望的结果，即从每个簇至少找出一个代表点。图2b显示随着样本容量从10变化到60时，从10个组的每一个得到一个对象的概率。有趣的是，使用容量为20的样本，只有很小的机会(20％)得到包含所有10个簇的样本。即便使用容量为30的样本，仍然有不小的机会(几乎40％)得到不包含所有10个簇中对象的样本。

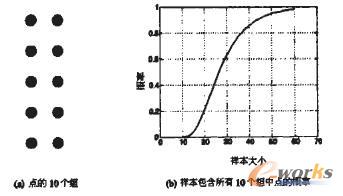
　　图2 从10个组找出具有代表性的点

　　6 结 论

　　本文提出了一种基于数据挖掘的启发式抽样方法，对传统分层抽样思想进行了改进。在后续工作中，我们将进一步结合具体事例，进行大量实验，对该方法进行证明。

　　本文创新点：结合了现有的数据挖掘技术与传统的统计学抽样发放；提出了一种启发式的抽样新思想，大大提高了抽取的样本的精确度与科学性。

转载：感谢您对网站平台的认可，以及对我们原创作品以及文章的青睐，非常欢迎各位朋友分享到个人站长或者朋友圈，但转载请说明文章出处。